Grand Unified Theory (syntax)
Grand Unified Theory (GUT) is successful in describing the four forces as distinct under normal circumstances, but connected in fundamental ways.
This section is referring to wiki page-26 of main section-4 that is inherited from the spin section-139 by prime spin-35 and span- with the partitions as below.
/syntax
- Addition Zones (0-18)
- Multiplication Zones (18-30)
- Exponentiation Zones (30-36)
- Identition Zones (36-102)
- Theory of Everything (span 12)
- Everything is Connected (span 11)
- Truncated Perturbation (span 10)
- Quadratic Polynomials (span 9)
- Fundamental Forces (span 8)
- Elementary Particles (span 7)
- Basic Transformation (span 6)
- Hidden Dimensions (span 5)
- Parallel Universes (span 4)
- Vibrating Strings (span 3)
- Series Expansion (span 2)
- Wormhole Theory (span 1)
GUT is also successful in describing a system of carrier particles for all four forces, but there is much to be done, particularly in the realm of gravity.
User Profiles
How can the Universe be so uniform? Now, the time for light to cross a significant part of the Universe is billions of years. We call this time the light communication time, and it is the shortest time required for any changes to be felt between two parts of the Universe. (From J. Schombert)
Unification
GUT predicts that the other forces become identical under conditions so extreme that they cannot be tested in the laboratory, although there may be lingering evidence of them in the evolution of the universe.
$True Prime Pairs:
(5,7$True Prime Pairs:
(5,7), (11,13), (17,19)
| 168 | 618 |
-----+-----+-----+-----+-----+ ---
19¨ | 3¨ | 4¨ | 6¨ | 6¨ | 4¤ -----> assigned to "id:30" 19¨
-----+-----+-----+-----+-----+ ---
17¨ | {5¨}| {3¨}| 2¨ | 7¨ | 4¤ -----> assigned to "id:31" |
+-----+-----+-----+-----+ |
{12¨}| 6¨ | 6¨ | 2¤ (M & F) -----> assigned to "id:32" |
+-----+-----+-----+ |
11¨ | 3¨ | {3¨}| {5¨}| 3¤ ---> Np(33) assigned to "id:33" -----> 👉 77¨
-----+-----+-----+----+-----+ |
19¨ | 4¨ | 4¨ | 5¨ | 6¨ | 4¤ -----> assigned to "id:34" |
+-----+-----+-----+-----+ |
{18¨}| ❓ | ❓ | ❓ | 3¤ ✔️ -----> assigned to "id:35" |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
43¨ | .. | .. | .. | .. | .. | .. | .. | .. | .. | 9¤ (C1 & C2) 43¨
-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
139¨ | 1 2 3 | 4 5 6 | 7 8 9 |
Δ Δ Δ
$True Prime Pairs:
(5,7$True Prime Pairs:
(5,7), (11,13), (17,19)
| 168 | 618 |
-----+-----+-----+-----+-----+ ---
19¨ | 3¨ | 4¨ | 6¨ | 6¨ | 4¤ -----> assigned to "id:30" 19¨
-----+-----+-----+-----+-----+ ---
17¨ | {5¨}| {3¨}| 2¨ | 7¨ | 4¤ -----> assigned to "id:31" |
+-----+-----+-----+-----+ |
{12¨}| 6¨ | 6¨ | 2¤ (M & F) -----> assigned to "id:32" |
+-👇--+-👇--+-----+ |
11¨ | 3¨ | {3¨}| {5¨}| 3¤ ---> Np(33) assigned to "id:33" -----> 👉 77¨
-----+-👇--+-👇--+----+-----+ |
19¨ | 4¨ | 4¨ | 5¨ | 6¨ | 4¤ -----> assigned to "id:34" |
+-----+-----+-----+-----+ |
{18¨}| ❓ | ❓ | .. | 3¤ ✔️ -----> assigned to "id:35" |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
43¨ | .. | .. | .. | .. | .. | .. | .. | .. | .. | 9¤ (C1 & C2) 43¨
-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
139¨ | 1 2 3 | 4 5 6 | 7 8 9 |
Δ Δ Δ
$True Prime Pairs:
(5,7$True Prime Pairs:
(5,7), (11,13), (17,19)
| 168 | 618 |
-----+-----+-----+-----+-----+ ---
19¨ | 3¨ | 4¨ | 6¨ | 6¨ | 4¤ -----> assigned to "id:30" 19¨
-----+-----+-----+-----+-----+ ---
17¨ | {5¨}| {3¨}| 2¨ | 7¨ | 4¤ -----> assigned to "id:31" |
+-----+-----+-----+-----+ |
{12¨}| 6¨ | 6¨ | 2¤ (M & F) -----> assigned to "id:32" |
+-👇--+-👇--+-👇--+ |
11¨ | 3¨ | {3¨}| {5¨}| 3¤ ---> Np(33) assigned to "id:33" -----> 👉 77¨
-----+-👇--+-👇--+-👇--+-----+ |
19¨ | 4¨ | 4¨ | 5¨ | 6¨ | 4¤ -----> assigned to "id:34" |
+-----+-----+-----+-----+ |
{18¨}| ❓ | ❓ | .. | 3¤ ✔️ -----> assigned to "id:35" |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
43¨ | .. | .. | .. | .. | .. | .. | .. | .. | .. | 9¤ (C1 & C2) 43¨
-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
139¨ | 1 2 3 | 4 5 6 | 7 8 9 |
Δ Δ Δ
$True Prime Pairs:
(5,7$True Prime Pairs:
(5,7), (11,13), (17,19)
| 168 | 618 |
-----+-----+-----+-----+-----+ ---
19¨ | 3¨ | 4¨ | 6¨ | 6¨ | 4¤ -----> assigned to "id:30" 19¨
-----+-----+-----+-----+-----+ ---
17¨ | {5¨}| {3¨}| 2¨ | 7¨ | 4¤ -----> assigned to "id:31" |
+-----+-----+-----+-----+ |
{12¨}| 6¨ | 6¨ | 2¤ (M & F) -----> assigned to "id:32" |
+-----+-----+-👇--+ |
11¨ | 3¨ | {3¨}| {5¨}| 3¤ ---> Np(33) assigned to "id:33" -----> 👉 77¨
-----+-----+-----+-👇--+-----+ |
19¨ | 4¨ | 4¨ | 5¨ | 6¨ | 4¤ -----> assigned to "id:34" |
+-👇--+-👇--+-----+-----+ |
{18¨}| 5¨ | 5¨ | .. | 3¤ ✔️ -----> assigned to "id:35" |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
43¨ | .. | .. | .. | .. | .. | .. | .. | .. | .. | 9¤ (C1 & C2) 43¨
-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
139¨ | 1 2 3 | 4 5 6 | 7 8 9 |
Δ Δ Δ
$True Prime Pairs:
(5,7$True Prime Pairs:
(5,7), (11,13), (17,19)
| 168 | 618 |
-----+-----+-----+-----+-----+ ---
19¨ | 3¨ | 4¨ | 6¨ | 6¨ | 4¤ -----> assigned to "id:30" 19¨
-----+-----+-----+-----+-----+ ---
17¨ | {5¨}| {3¨}| 2¨ | 7¨ | 4¤ -----> assigned to "id:31" |
+-----+-----+-----+-----+ |
{12¨}| 6¨ | 6¨ | 2¤ (M & F) -----> assigned to "id:32" |
+-----+-----+-----+ |
11¨ | 3¨ | {3¨}| {5¨}| 3¤ ---> Np(33) assigned to "id:33" -----> 👉 77¨
-----+-----+-----+-----+-----+ |
19¨ | 4¨ | 4¨ | 5¨ | 6¨ | 4¤ -----> assigned to "id:34" |
+-----+-----+-----+-----+ |
{18¨}| 5¨ | 5¨ | 8¨ | 3¤ ✔️ -----> assigned to "id:35" |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
43¨ | .. | .. | .. | .. | .. | .. | .. | .. | .. | 9¤ (C1 & C2) 43¨
-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ ---
139¨ | 1 2 3 | 4 5 6 | 7 8 9 |
Δ Δ Δ
Black Hole
E = mc²
m = E = mc²
m = E/c²
c = 1 light-second
= 1000 years x L / t
= 12,000 months x 2152612.336257 km / 86164.0906 sec
= 299,792.4998 km / sec
Note:
1 year = 12 months
1000 years = 12,000 months
Te = earth revolution = 365,25636 days
R = radius of moon rotation to earth = 384,264 km
V = moon rotation speed = 2πR/Tm = 3682,07 km/hours
Ve = excact speed = V cos (360° x Tm/Te) = V cos 26,92848°
Tm = moon revolution (sidereal) = 27,321661 days = 655,719816 hours
t = earth rotation (sinodik) = 24 hours = 24 x 3600 sec = 86164.0906 sec
L = Ve x Tm = 3682,07 km/hours x cos 26,92848° x 655,71986 = 2152612.336257 km
Conclusion:
π(π(π(π(π(32(109²-89²)))))) Universe vs Parallel vs Multiverse (via blackhole)
👇
π(π(π(π(32(109²-89²))))) Galaxies vs Universe vs Parallel (gap in 2nd-level)
👇
π(π(π(32(109²-89²)))) Sun vs Galaxies vs Universe (2nd gap in 1st-level)
👇
π(π(32(109²-89²))) Moon vs Sun vs Galaxies (1st-gap via dark matter)
👇
|--👇---------------------------- 2x96 ---------------------|
|--👇----------- 7¤ ---------------|---------- 5¤ ----------|
|- π(32(109²-89²))=109² -|-- {36} -|-------- {103} ---------|
+----+----+----+----+----+----+----+----+----+----+----+----+
| 5 | 7 | 11 |{13}| 17 | 19 | 17 |{12}| 11 | 19 | 18 |{43}|
+----+----+----+----+----+----+----+----+----+----+----+----+
|--------- {53} ---------|---- {48} ----|---- {48} ----|109²-89² 👉 Unknown
|---------- 5¤ ----------|------------ {96} -----------|-1¤-|
|-------- Bosons --------|---------- Fermions ---------|-- Graviton
|-- Sun Orbit (7 days) --|--- Moon Orbit (12 months) --| (11 Galaxies)
|------------ Part of 1 Galaxy (Milky Way) ------------| Non Milky Way 👉 Σ=12
How water is formed
Finally, there exist scenarios in which there could actually be more than 4D of spacetime. String theories require extra dimensions of spacetime for their mathematical consistency. In string theory, spacetime is 26-dimensional, while in superstring theory it is 10-dimensional, and in M-theory it is 11-dimensional.
These are situations where theories in two or three spacetime dimensions are no more useful. This classification theorem identifies several infinite families of groups as well as 26 additional groups which do not fit into any family. (Wikipedia)
[(6 + 6) x 6] + [6 + (6 x 6)] = 72 + 42 = 71 + 42 + 1 = 114 objects
The Prime Recycling ζ(s):
(2,3), (29,89), (36,68), (72,42), (100,50), (2,3), (29,89), ...**infinity**
----------------------+-----+-----+-----+ ---
7 --------- 1,2:1| 1 | 30 | 40 | 71 (2,3) ‹-------------@---- |
| +-----+-----+-----+-----+ | |
| 8 ‹------ 3:2| 1 | 30 | 40 | 90 | 161 (7) ‹--- | 5¨ encapsulation
| | +-----+-----+-----+-----+ | | |
| | 6 ‹-- 4,6:3| 1 | 30 | 200 | 231 (10,11,12) ‹--|--- | |
| | | +-----+-----+-----+-----+ | | | ---
--|--|-----» 7:4| 1 | 30 | 40 | 200 | 271 (13) --› | {5®} | |
| | +-----+-----+-----+-----+ | | |
--|---› 8,9:5| 1 | 30 | 200 | 231 (14,15) ---------› | 7¨ abstraction
289 | +-----+-----+-----+-----+-----+ | |
| ----› 10:6| 20 | 5 | 10 | 70 | 90 | 195 (19) --› Φ | {6®} |
--------------------+-----+-----+-----+-----+-----+ | ---
67 --------› 11:7| 5 | 9 | 14 (20) --------› ¤ | |
| +-----+-----+-----+ | |
| 78 ‹----- 12:8| 9 | 60 | 40 | 109 (26) «------------ ✔️ | 11¨ polymorphism
| | +-----+-----+-----+ | | |
| | 86‹--- 13:9| 9 | 60 | 69 (27) «-- Δ19 (Rep Fork) | {2®} | |
| | | +-----+-----+-----+ | | ---
| | ---› 14:10| 9 | 60 | 40 | 109 (28) ------------- | |
| | +-----+-----+-----+ | |
| ---› 15,18:11| 1 | 30 | 40 | 71 (29,30,31,32) ---------- 13¨ inheritance
329 | +-----+-----+-----+ |
| ‹--------- 19:12| 10 | 60 | {70} (36) ‹--------------------- Φ |
-------------------+-----+-----+ ---
786 ‹------- 20:13| 90 | 90 (38) ‹-------------- ¤ |
| +-----+-----+ |
| 618 ‹- 21,22:14| 8 | 40 | 48 (40,41) ‹---------------------- 17¨ class
| | +-----+-----+-----+-----+-----+ | |
| | 594 ‹- 23:15| 8 | 40 | 70 | 60 | 100 | 278 (42) «-- |{6'®} |
| | | +-----+-----+-----+-----+-----+ | | ---
--|--|-»24,27:16| 8 | 40 | 48 (43,44,45,46) ------------|---- |
| | +-----+-----+ | |
--|---› 28:17| 100 | {100} (50) ------------------------» 19¨ object
168 | +-----+ |
| 102 -› 29:18| 50 | 50(68) ---------> Δ18 |
----------------------+-----+ ---
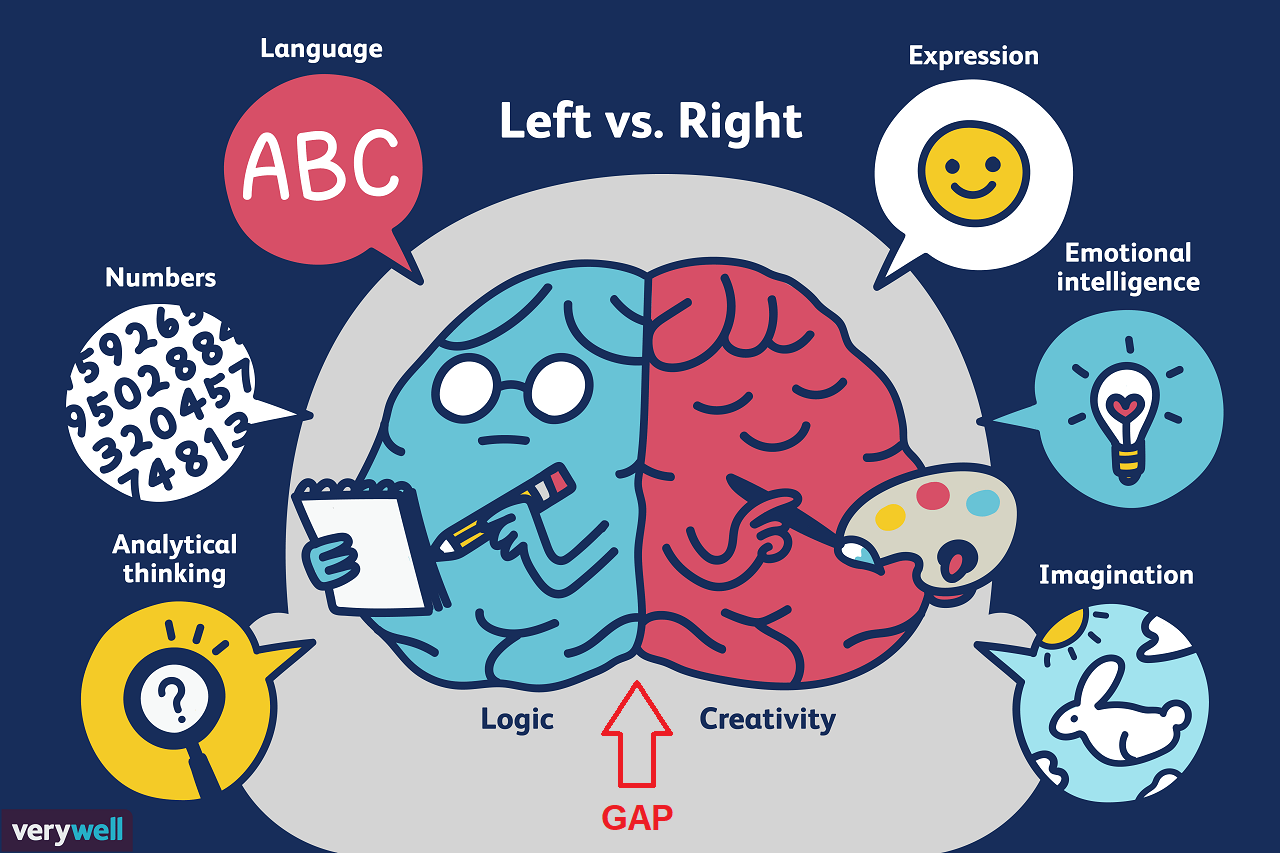
The only different is, instead of an instance, it will behave as an inside container, just like how spider built a home web as strong as steel but useless to cover them against a rainy day nor even a small breeze.
This would even close to the similar ability of human brain without undertanding of GAP functionality between left and right of the human brain.
Final Theory
Prime Identity
We are going to assign prime identity as a standard model that attempts to stimulate a quantum field model called eQuantum for the four (4) known fundamental forces.
This section is referring to wiki page-26 of main section-4 that is inherited from the spin section-139 by prime spin-35 and span- with the partitions as below.
/syntax
- Addition Zones (0-18)
- Multiplication Zones (18-30)
- Exponentiation Zones (30-36)
- Identition Zones (36-102)
- Theory of Everything (span 12)
- Everything is Connected (span 11)
- Truncated Perturbation (span 10)
- Quadratic Polynomials (span 9)
- Fundamental Forces (span 8)
- Elementary Particles (span 7)
- Basic Transformation (span 6)
- Hidden Dimensions (span 5)
- Parallel Universes (span 4)
- Vibrating Strings (span 3)
- Series Expansion (span 2)
- Wormhole Theory (span 1)
This presentation was inspired by theoretical works from Hideki Yukawa who in 1935 had predicted the existence of mesons as the carrier particles of strong nuclear force.
Addition Zones
Here we would like to recompile the way we take on getting the arithmetic expresion of an individual unit expression (identity) such as a taxicab number below.
It is a taxicab number, and is variously known as Ramanujan’s number and the Ramanujan-Hardy number, after an anecdote of the British mathematician GH Hardy when he visited Indian mathematician Srinivasa Ramanujan in hospital (Wikipedia).
These three (3) number are twin primes. We called the pairs as True Prime Pairs. Our scenario is mapping the distribution out of these pairs by taking the symmetrical behaviour of 36 as the smallest power (greater than 1) which is not a prime power.
The smallest square number expressible as the sum of four (4) consecutive primes in two ways (5 + 7 + 11 + 13 and 17 + 19) which are also two (2) couples of prime twins! (Prime Curios!).
$True Prime Pairs:
(5,7), (11,13), (17,19)
layer| i | f
-----+-----+---------
| 1 | 5
1 +-----+
| 2 | 7
-----+-----+--- } 36 » 6®
| 3 | 11
2 +-----+
| 4 | 13
-----+-----+---------
| 5 | 17
3 +-----+ } 36 » 6®
| 6 | 19
-----+-----+---------
Thus in short this is all about the method that we called as the 19 vs 18 Scenario of mapping the quantum way within a huge of primes objects (5 to 19) by lexering (11) the ungrammared feed (7) and parsering (13) across syntax (17).
Φ(1,2,3) = Φ(6,12,18) = Φ(13,37,61)
$True Prime Pairs:
(5,7), (11,13), (17,19)
layer | node | sub | i | f
------+------+-----+----------
| | | 1 |
| | 1 +-----+
| 1 | | 2 | (5)
| |-----+-----+
| | | 3 |
1 +------+ 2 +-----+----
| | | 4 |
| +-----+-----+
| 2 | | 5 | (7)
| | 3 +-----+
| | | 6 |
------+------+-----+-----+------ } (36)
| | | 7 |
| | 4 +-----+
| 3 | | 8 | (11)
| +-----+-----+
| | | 9 |
2 +------| 5 +-----+-----
| | | 10 |
| |-----+-----+
| 4 | | 11 | (13)
| | 6 +-----+
| | | 12 |
------+------+-----+-----+------------------
| | | 13 |
| | 7 +-----+
| 5 | | 14 | (17)
| |-----+-----+
| | | 15 |
3 +------+ 8 +-----+----- } (36)
| | | 16 |
| |-----+-----+
| 6 | | 17 | (19)
| | 9 +-----+
| | | 18 |
------|------|-----+-----+------
The main background is that, as you may aware, the prime number theorem describes the asymptotic distribution of prime numbers which is still a major problem in mathematic.
Multiplication Zones
Instead of a proved formula we came to a unique expression called zeta function. This expression first appeared in a paper in 1737 entitled Variae observationes circa series infinitas.
This expression states that the sum of the zeta function is equal to the product of the reciprocal of one minus the reciprocal of primes to the powers. But what has this got to do with the primes? The answer is in the following product taken over the primes p (discovered by Leonhard Euler):
This issue is actually come from Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is considered to be the most important of unsolved problems in pure mathematics.
In addition to the trivial roots, there also exist complex roots for real t. We find that the he first ten (10) non-trivial roots of the Riemann zeta function is occured when the values of t below 50. A plot of the values of ζ(1/2 + it) for t ranging from –50 to +50 is shown below. The roots occur each time the locus passes through the origin. (mathpages).
Meanwhile obtaining the non complex numbers it is easier to look at a graph like the one below which shows Li(x) (blue), R(x) (black), π(x) (red) and x/ln x (green); and then proclaim "R(x) is the best estimate of π(x)." Indeed it is for that range, but as we mentioned above, Li(x)-π(x) changes sign infinitely often, and near where it does, Li(x) would be the best value.
And we can see in the same way that the function Li(x)-(1/2)Li(x1/2) is ‘on the average' a better approximation than Li(x) to π(x); but no importance can be attached to the latter terms in Riemann's formula even by repeated averaging.
Exponentiation Zones
The problem is that the contributions from the non-trivial zeros at times swamps that of any but the main terms in these expansions.
A. E. Ingham says it this way: Considerable importance was attached formerly to a function suggested by Riemann as an approximation to π(x)… This function represents π(x) with astonishing accuracy for all values of x for which π(x) has been calculated, but we now see that its superiority over Li(x) is illusory… and for special values of x (as large as we please) the one approximation will deviate as widely as the other from the true value (primes.utm.edu).
Moreover in it was verified numerically, in a rigorous way using interval arithmetic, that The Riemann hypothesis is true up to 3 · 10^12. That is, all zeroes β+iγ of the Riemann zeta-function with 0<γ≤3⋅1012 have β=1/2.
We have Λ ≤ 0.2. The next entry is conditional on taking H a little higher than 10*13, which of course, is not achieved by Theorem 1. This would enable one to prove Λ < 0.19. Given that our value of H falls between the entries in this table, it is possible that some extra decimals could be wrought out of the calculation. We have not pursued this (arXiv:2004.09765).
This Euler formula represents the distribution of a group of numbers that are positioned at regular intervals on a straight line to each other. Riemann later extended the definition of zeta(s) to all complex numbers (except the simple pole at s=1 with residue one). Euler's product still holds if the real part of s is greater than one. Riemann derived the functional equation of zeta function.
The Riemann zeta function has the trivial zeros at -2, -4, -6, … (the poles of gamma(s/2)). Using the Euler product (with the functional equation) it is easy to show that all the other zeros are in the critical strip of non-real complex numbers with 0 < Re(s) < 1, and that they are symmetric about the critical line Re(s)=1/2. The unproved Riemann hypothesis is that all of the nontrivial zeros are actually on the critical line (primes.utm.edu).
If both of the above statements are true then mathematically this Riemann Hypothesis is proven to be incorrect because it only applies to certain cases or limitations. So first of all the basis of the Riemann Hypothesis has to be considered.
The solution is not only to prove Re(z)= 1/2 but also to calculate ways for the imaginary part of the complex root of ζ(z)=0 and also to solve the functional equations. (Riemann Zeta - pdf)
On the other hand, the possibility of obtaining the function of the distribution of prime numbers shall go backwards since it needs significant studies to be traced.
Or may be start again from the Euleur Function.
Identition Zones
Freeman Dyson discovered an intriguing connection between quantum physics and Montgomery's pair correlation conjecture about the zeros of the zeta function which dealts with the distribution of primes.
The Mathematical Elementary Cell 30 (MEC30) standard unites the mathematical and physical results of 1972 by the mathematician Hugh Montgomery and the physicist Freeman Dyson and thus reproduces energy distribution in systems as a path plan more accurately than a measurement. (Google Patent DE102011101032A9)
The path plan assume that a symmetric distribution of prime numbers with equal axial lengths from a middle zero axis = 15 is able to determine the distribution of primes in a given number space. This assumption finally bring us to the equation of Euler's identity.
Euler’s identity is considered to be an exemplar of deep mathematical beauty as it shows a profound connection between the most fundamental numbers. Three (3) of the basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation (Wikipedia).
The finiteness position of Euler's identity by the said MEC30 opens up the possibility of accurately representing the self-similarity based on the distribution of True Prime Pairs so that all number would belongs together with their own identitities.
The structure is arranged based on 11 dimensions of space and time which is composed of 12 loops woven into the spin networks.
The result should be a massive neutrinos that bring 7 more parameters (3 CKM and 4 PMNS) for a total of 26 parameters out of 11+26=37 symmetry.
Schematic representation of fermions and bosons in SU(5) GUT showing 5 + 10 split in the multiplets. Neutral bosons (photon, Z-boson, and neutral gluons) are not shown but occupy the diagonal entries of the matrix in complex superpositions.
And, speaking of the Fibonacci number sequence, there is symmetry mirroring the above in the relationship between the terminating digits of Fibonacci numbers and their index numbers equating to members of the array populating the Prime Spiral Sieve:
The 10 symmetries are reflecting the 10 shapes of the chart as shown below. The 12 finite loops around the three (3) generation are denoted by the total of 12 arrows that flowing in between each of the 10 shapes.
Nothing is going to be easly about the nature of prime numbers but they demonstrably congruent to something organized. Let's discuss starting with the addition zones.
eQuantum Project
Copyright © 2023-2024
Reference:
